Musterlösung Aufgabenblatt 0
Dies ist eine Musterlösung für das Aufgabenblatt 0. Sie enthält alles, was für eine volle Punktzahl erforderlich ist und soll als Beispiel/Vorlage für Folgeaufgaben dienen.
Aufgabe 1
Problemanalyse
Was macht das Problem kompliziert?
Auf den ersten Blick sieht es aus, als müsste man den Pfad der Zahlenschlange schrittweise nachempfinden, um zum gewünschten Punkt zu kommen. Die Puzzleeingabe ist allerdings so groß, dass dies nicht möglich erscheint.
Skizzieren Sie, falls möglich, einen naiven brute-force Lösungsansatz und ermitteln seine Laufzeit in O-Notation und seinen Speicherbedarf.
Siehe dazu auch die Vorlesungsunterlagen.
Hier nun die manuelle Komplexitätsanalyse eines Brute-Force Ansatzes:
#include <cstdint>
#include <iostream>
#include <gmp.h>
#include <gmpxx.h>
int main(){
mpz_class input;
cin << input; // Zuweisung: Konstante Zeit, pauschal eine Zeiteinheit
mpz_class line = 0; // Zuweisung: Konstante Zeit, pauschal eine Zeiteinheit
mpz_class linesize = 1; // Zuweisung: Konstante Zeit, pauschal eine Zeiteinheit
mpz_class i = 0; // Zuweisung: Konstante Zeit, pauschal eine Zeiteinheit
/*
* Schleife läuft in Abhängigkeit zur Eingabe, aber in leicht modifizierter Abhängigkeit.
* Die Schleife läuft so oft, wie die Wurzel des Eingabewerts -> n^(1/2)
* Der Komplexitätszuwachs wird gemessen in Abhängigkeit vom Wachstum der Eingabegröße, *nicht* dem Eingabewert!
* In welchem Stellensystem die Eingabegröße wächst, ist für Zwecke der O-Notation irrelevant.
* Beispiel: Nehmen wir das Binärsystem, dann verdoppelt sich mit jedem Wachstumsschritt der Eingabewert.
* Kontinuierliches Verdoppeln kann man wie folgt schreiben:
* 2*2*2*2*2*... -> 2^n -> Exponentielles Wachstum des Eingabewerts
* Die Wurzel von 2^n ist 2^(n/2), was immer noch exponentiell wächst.
*/
while(i < input){
i += linesize; // Addition: Eine Zeiteinheit
line++; // Addition: Eine Zeiteinheit
linesize += 2; // Addition: Eine Zeiteinheit
}
mpz_class line_middle = line*line - line + 1; // Multiplikation, Subtraktion, Addition: Drei Zeiteinheiten
mpz_class column = input - line_middle; // Subtraktion: Eine Zeiteinheit
column = abs(column); // Absolutwert: Triviale konstante Operation - Pauschal eine Zeiteinheit
line--; // Subtraktion: Eine Zeiteinheit
mpz_class result = line+column; // Addition: Eine Zeiteinheit
cout << result << endl; // Irrelevant, nicht Teil des Algorithmus
return 0; // Irrelevant, nicht Teil des Algorithmus
}
Beschreiben Sie ihren Lösungsansatz
Beschreiben Sie eingesetzte Algorithmen/Lösungsstrategien und Datenstrukturen. Zitieren Sie Sekundärquellen, die zur Lösung beigetragen haben.
Erkenntnis: Der horizontale Verlauf der Zahlen ist irrelevant, sie könnten genausogut jedes Mal von links nach rechts gehen und es würde nichts an der Distanz zum Feld 1 ändern.
Eine Suche in OEIS zeigt, dass jede Zahlenreihe mit der nächstfolgenden Quadratzahl endet. Wir können also die Ebene ermitteln, indem wir die ganzzahlige Wurzel des Puzzleinputs bilden.
Die weitere Erkenntnis ist, dass die horizontale Mitte der Zahlenebene sich aus dem Durchschnitt der Quadratzahl dieser Ebene und der Quadratzahl der vorherigen Ebene plus Eins bilder.
Ermitteln Sie die Laufzeit Ihrer Lösung in O-Notation.
Manuelle Komplexitätsanalyse:
#include <cmath>
#include <cstdint>
#include <iostream>
#include <string>
#include <gmp.h>
#include <gmpxx.h>
using namespace std;
void solve(string input_line){
mpz_class input(input_line);
/*
* Determine the line. Basically, each line
* represents the range from 2^(n-1) to 2^n,
* with an offset of 1.
*/
mpz_class line;
mpz_class input_x = input - 1; // Subtraktion: Konstante Zeit, pauschal eine Zeiteinheit
mpz_sqrt(line.get_mpz_t(), input_x.get_mpz_t()); // Ganzzahlige Wurzel: Lt. GMP Dokumentation log(log(n))
/*
* Determine the column. Find the value of the middle,
* then subtract the input, take the absolute value, presto.
*/
mpz_class line_squared;
mpz_pow_ui(line_squared.get_mpz_t(), line.get_mpz_t(), 2); // Multiplikation: Konstante Zeit, pauschal eine Zeiteinheit
mpz_class line_middle_2 = line_squared + line + 1; // Addition: Konstante Zeit, pauschal eine Zeiteinheit
mpz_class diff = input - line_middle_2; // Subtraktion: Konstante Zeit, pauschal eine Zeiteinheit
mpz_class column = abs(diff); // Absolutwert: Konstante Zeit, pauschal eine Zeiteinheit
mpz_class result = line + column; // Addition: Konstante Zeit, pauschal eine Zeiteinheit
cout << result << endl;
}
int main(){
// Read the input from stdin
for(string line;getline(cin,line);){
solve(line);
}
return 0;
}
Da diese Lösung komplett ohne Schleifen auskommt (und wir es etwas genauer wissen wollen), müssen wir uns die einzelnen Operationen genauer ansehen. Die kompliziertesten Operationen sind:
- Die Multiplikation (O(n*log(n) Quelle)
- Die Ganzzahlige Wurzel ist in der GMP Library an die Multiplikation gekoppelt Quelle
Damit kann man für die Komplexität des Algorithmus O(M(n)), wobei M(n) für die Komplexität der Multiplikation steht.
Messen Sie die Laufzeit Ihres Programms auf einem Laborrechner der Hochschule. Verändern Sie, wenn es die Aufgabenstellung erlaubt, die Eingabegröße und messen Sie erneut.
Die Aufgabenstellung erlaubt natürlich beliebige andere Zahlen. Wichtig dabei: Zahlenwert != Eingabegröße.
Dieses Beispielskript startet ein Programm in einer Schleife mit Zahlen in wachsender Größenordnung:
#!/usr/bin/env python3
import subprocess
import time
import random
import sys
from subprocess import *
uut = sys.argv[1]
input_val = 2
for i in range(0,1600000,100000):
proc_uut = subprocess.Popen([uut],stdin=PIPE, stdout=PIPE)
input = str((2**(i+1))-1) + "\n"
before = time.monotonic()
out_uut = proc_uut.communicate(input.encode(), timeout=60)[0].decode()
after = time.monotonic()
time_uut = after-before
out_uut = out_uut.strip()
print("{};{}".format(i,time_uut))
Das Programm erhöht die Größenordnung schrittweise um 100000 Binärstellen, um auch nur annähernd ein Wachstum zu bemerken.
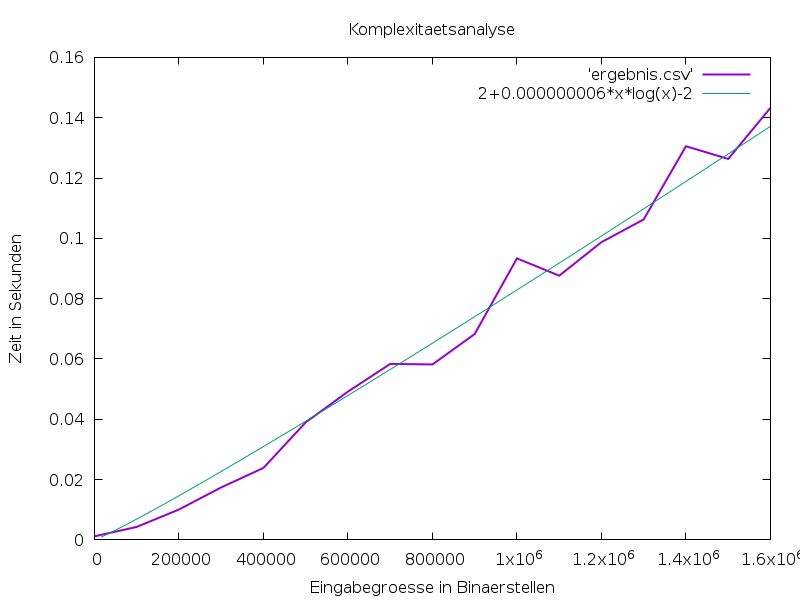
0;0.0011960369993175846
100000;0.004318690000218339
200000;0.010086661999594071
300000;0.01740139599860413
400000;0.02386787099931098
500000;0.03898440900047717
600000;0.04917196499991405
700000;0.05835848099923169
800000;0.058187200000247685
900000;0.06827419099863619
1000000;0.09335216900035448
1100000;0.087615905000348
1200000;0.09872929199991631
1300000;0.10628582599929359
1400000;0.1305392740014213
1500000;0.12632678599948122
1600000;0.14329079200069827
Mit Gnuplot legen wir eine n*log(n) Funktion nebenbei als Vergleichswert:
#!/usr/bin/env gnuplot
set datafile separator ";"
set title "Komplexitaetsanalyse"
set ylabel "Zeit in Sekunden"
set xlabel "Eingabegroesse in Binaerstellen"
set terminal pngcairo size 800,600
set output 'ergebnis.png'
plot 'ergebnis.csv' with lines lw 2, 2+0.000000006*x*log(x)-2 with lines
Das Ergebnis ist hier zu sehen: